
1 Indian Institute of Foreign Trade, Kolkata Campus, Kolkata, West Bengal, India
This article analyses interest rate pass-through in India using nonlinear autoregressive distributed lag (NARDL) model. The results suggest the rejection of decoupling hypothesis of interest rates. The results show evidence of cointegration between the policy rates and all other market interest rates. We find evidence of near complete, relatively rapid and asymmetric pass-through from policy rates to the immediate monetary policy target in India, that is, call money rates. However, we find evidence of incomplete, sluggish and asymmetric pass-through from policy rates to both long-term market interest rates and lending rates.
Interest rate, monetary policy, cointegration, NARDL
Introduction
The relationship between policy-regulated interest rates and longer-term market interest rates is elemental to the operation of monetary policy. There is almost a similar monetary policy operating procedure adopted worldwide. The central bank of a country sets the policy rates which are aimed to directly affect the market interest rates. The successful transmission of these policy changes is supposed to affect real economic activity through different channels, popularly known as ‘transmission mechanism of monetary policy’. Money market has a pivotal role in monetary transmission as money market interest rates are the first or immediate targets of monetary policy. Central banks intently observe and affect money market developments as they are the most important and critical link through which monetary policy influences the final targets of price stability and output (Becker et al., 2012). Since central banks have limited control over long-term interest rates which are supposed to affect real economic activity via investment and expenditure decisions, the central bank regulates these rates via signalling mechanism. Due to the presence of asymmetric information and other market rigidities in financial markets, signalling is an effectual mechanism of overcoming the asymmetry and successfully transmit the central bank’s policy stance to the market. The policy stance via signalling indicates the intention of policymakers and their future outlook on macroeconomy. The signalling mechanism tends to be strong in developed economies owing to well-developed financial systems. In emerging market economies due to various reasons like market segmentation and weak monetary transmission, the signalling mechanism is very weak. In the backdrop of this weak signalling mechanism, there are continuous changes in the framework and operating procedure of monetary policy in these economies to increase the efficacy of policy actions. One such important change was the emphasis by central banks on price channels by early 1980s. The price channel is the use of short-term interest rates to manage liquidity in the system. This change in the operating framework made money market developments more important from transmission point of view.
Amidst the changes in monetary policy framework, it becomes imperative to study the effects of policy actions on intermediate and subsequently on final goals in order to have an enhanced and clearer picture about the transmission of policy actions. As it is known that central banks influence both the cost and quantity of liquidity through changes in policy rates, financial markets respond to these policy changes and adjust different rates of return on their assets. This response of market interest rates to changes in policy-administered interest rates is called interest rate pass-through. A complete pass-through from policy rates to market interest rates is a sign of sound and competitive financial system. An incomplete pass-through is an indication of stickiness or market rigidity. The success of monetary policy in achieving its goals depends on the stickiness or interest rate rigidity present in the market. The changes in official policy rates affect the market interest rates to varying degrees or in other words, there is no one-to-one relation as expected. There is a growing literature which points towards the incomplete pass-through. The empirical literature also points towards asymmetric pass-through; that is, rate cuts and rate hikes (of policy rate) do not have equal effect. The theoretical explanations of incomplete and asymmetric interest-rate pass-through provided by literature include implicit contracting, imperfect competition in banking sector, asymmetric information, long-term bank-client relationship, menu costs, economic conditions, risk sharing and switching costs (De Bondt, 2002; Francesco & José, 2015). In this article, our main focus is to empirically test these assumptions in monetary theory regarding monetary policy like the pass-through from central bank policy rates to market interest rates is complete (i.e., there is a one-to-one relation) and symmetric (i.e., reaction towards rate cuts and hikes are equal).
Literature Review
While there is ample theoretical as well as empirical literature on efficacy of monetary policy transmission, the incompleteness and asymmetric pass-through of policy rates have been more or less an under-investigated area. In this section, we will review some important studies which have focused on different aspects of interest-rate pass-through.
To begin with, we need to look at the two stages of pass-through. The first stage is the transmission of policy rates to short-term and long-term money market interest rates and the second stage is the transmission from money market to commercial lending and deposit rates. The first stage is largely influenced by the stability of yield curve over time. If the term structure of interest rates remains stable over time, then pass-through from policy rates to market rates may be proportionate, otherwise, any twiddle changes the scenario (Égert et al., 2007). The first important study to look into interest rate pass-through in the second stage is perhaps by Fried and Howitt (1980), who showed that interest rate rigidity arises because of risk-sharing agreements between banks and their customers. The pioneering work in this area can be seen as that of Stiglitz and Weiss (1981). They explained interest rate rigidity in terms of asymmetric information. According to them, banks maintain a large spread in perception of high default risk, and given that information asymmetry leads to adverse selection in loan markets, any rate increase from monetary authority if matched by banks would increase the loan default probability, because higher interest rates attract riskier borrowers. Thus, instead of raising rates on loans, banks maintain equilibrium through credit rationing. This may lead to upward rigidity and asymmetric adjustment in lending rates. Rotemberg and Saloner (1987) explained the phenomena of interest rate rigidity in terms of menu costs theory. According to them as long as policy rate changes are small and perceived as temporary, pass-through may be delayed and in some cases missing altogether. Lowe and Rohling (1992) explained the interest rate rigidity in terms of switching costs. According to them, higher switching costs can be a demotivating factor for customers to change banks. This factor is exploited by banks in terms of asymmetric or incomplete pass-through. In a similar study, Berger and Udell (1992) showed how implicit contracts and other kinds of agreements make interest rate pass-through stickier and asymmetric. Bernanke et al. (1996) showed how in presence of asymmetric information, financial frictions lead to overpass-through from policy to retail rates. On overpass-through, De Bondt (2005) highlighted different reasons. He explains that instead of credit rationing, banks increase lending rates more than those dictated by the monetary authority. This more than proportionate change can be seen as compensation for increasing probability of loan default from a rate hike. Kwapil and Scharler (2006) provide a detailed survey of literature on interest rate pass-through. Some general conclusions emerging from that study are that pass-through from policy rates to market rates is both sluggish and incomplete. Other important findings from that survey point that degree of pass-through decreases with increasing maturity. Égert et al. (2007, 2009) highlighted the role of macroeconomic environment in affecting interest rate rigidity. According to these studies, favourable macroeconomic condition like high economic growth prompt banks to pass on policy changes quickly as risk of default is low or in other words probability of repayment is high.
The other important aspect of pass-through we are interested in testing is the asymmetry. The theoretical underpinning of asymmetry lies in collusive behaviour of banks. There are two hypotheses which explain the asymmetry of pass-through, namely collusive behaviour hypothesis and adverse customer reaction hypothesis. According to collusive behaviour, hypothesis imperfect competition in banking or collusive agreements leads to asymmetric pass-through. Thus, there will be an upward rigidity in deposit rates following a policy rate hike and there will be downward rigidity in lending rates following a policy rate cut. The reason for upward rigidity in deposit rates being that higher deposit rates mean increased costs for banks or in other words lower profits. And the reason for downward rigidity in lending rates is that if lending rates are decreased following a policy rate cut, the lower lending rates simply mean lower profit earnings for banks. The adverse customer reaction hypothesis states that in a highly competitive environment, customers have bargaining power. Fearing a negative backlash in terms of losing customers to other banks who may not follow the suit (change their deposit and lending rates following policy changes), banks may choose not to pass on the policy changes symmetrically to the customers. There are other hypotheses which explain the asymmetric pass-through like adverse selection and switching costs hypothesis which we already discussed.
Although empirical literature indicates presence of asymmetry in pass-through, but the exact forms of asymmetry are not clear as there is a dearth of studies which have studied nonlinearities in pass-through in a meticulous manner. Among the early studies on asymmetry of pass-through, Borio and Fritz (1995), while studying interest rates for various OCED economies using ECM models, found positive short-run asymmetry from market rates to lending rates. Gual (1999) while studying interest rates in some European economies found evidence of negative short-run asymmetry. His findings suggested that due to competition, banks tend to adjust lending rates more quickly when market interest rates are declining than when they are rising. Dueker (2000) analysed the US data on interest rates using ordered probit models and concludes that there is positive long-run asymmetry from policy rates to long-term interest rates. Contrary to this Sellon (2002) provided evidence of long-run negative asymmetric pass-through from policy rates to mortgage rates in the US. Sander and Kleimeier (2004), using a nonlinear ECM for Euro Area, found rigidity in upward and downward adjustments. They found upward adjustment to be faster than downward adjustments for majority of countries under study. In a recent study by Greenwood-Nimmo et al. (2013), while analysing US monetary policy pass-through under different regimes, the authors found mixed evidence for positive short-run and negative long-run asymmetry. Also, the study confirms sluggishness and incompleteness in pass-through from policy rates to long-term market interest rates.
Now turning towards the studies on India, India has been a part of various panel studies on interest rate pass-through, the results of which have no consensus. For example, Karagiannis et al. (2009) while studying interest rate pass-through in BRIC1 countries found variations across the panel. However, for India, the authors found complete pass-through in the long run. In contrast, Guimaraes and Ruiz-Arranz (2009) while studying pass-through in nine Asia-Pacific economies found incomplete pass-thorough in the Indian case; precisely they found the pass-through coefficient to be 0.3. A similar result was found by Hattari et al. (2011); while studying pass-through for four Asian economies2, they found the long-run pass-through coefficient to be 0.3 for India.
While the above-reviewed studies were panel studies where the results have no consensus and individual country effects are not taken care of, we turn towards the studies which exclusively focused on India. The Currency and Finance Report of Reserve Bank of India (RBI) (2003–04) found an incomplete interest rate pass-through, precisely the pass-through coefficients were 0.61 for lending rates and 0.42 for deposit rates and hence confirming rigidity in response to rate changes. The report also found pass-through coefficients showed increasing signs over time thus showing signs of improving transmission. Bhattacharyya and Sensarma (2008), while studying various signalling instruments of RBI, found the changes in principal signalling instrument from pre-LAF to post-LAF period.3 The study by Bhattacharyya and Sensarma (2008) further showed that cash reserve ratio (CRR) is the dominant instrument in pre-LAF while the repo rate became dominant tool in the post-LAF. The study concluded that RBI’s policy actions have considerable influence over various segments of financial markets in India, but the impact on stock markets is insignificant. The study overall concluded that new tools of monetary policy have better impact on overall transmission. Singh (2011) while studying pass-through from policy rates to various market interest rates found lagged effects in the pass-through thus confirming incomplete and sluggishness in the pass-through. Recently there have been two important studies which studied the interest rate pass-through in India as two-stage process. The first stage is pass-through from policy rates to immediate target (money market interest rates) and the second stage is from immediate target to market interest rates. The first study is by Das (2015), which studied the credit channel of monetary policy in India. The main findings of this study are that in the first stage, there is almost complete pass-through from repo rate to WACMR (weighted average of call money rates; immediate target of monetary policy in India), while pass-through from reverse repo and CRR was either incomplete or insignificant. In the second stage, the study found evidence of slow and asymmetric pass-through to bank interest rates in India. Specifically tight monetary policy leads to more quick adjustment in lending rates than monetary expansion. The second study is by Rajan and Yanamandra (2015), which studied pass-through as a two-stage process. The study found evidence of complete pass-through in the first stage, that is, from policy rate to interbank rates; and incomplete pass-through in the second stage, that is, to lending rates. The study, however, refrains from saying that monetary policy is ineffective as the lending rates and policy rates showed co-movement in the same direction.
After reviewing the available studies in general and those focusing on India, we found that the asymmetric aspect of interest rate pass-through has not been studied in a rigorous manner, particularly in the Indian context. Hence, this study is an attempt to fill this gap at an empirical level.
Data Description and Empirical Method
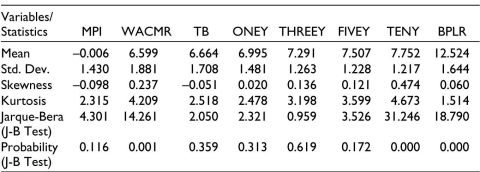
In this article, we examine the pass-through of RBI’s rate changes to market interest rates (short-term and long-term) as well as to lending rates. The study uses monthly data from June 2000 to March 2020. The stance of monetary policy is measured by a composite index constructed by principal component analysis (PCA; discussed in detail in next section). The index of monetary policy stance (hereafter MPI) was constructed by using data on repo, reverse repo and CRR. For short-term interest rates, two variables namely WACMR and 91 days treasury bills (TB) are used. For long-term interest rates, data on government securities (hereafter G-Sec) of various maturities – one year (ONEY), three years (THREEY), five years (FIVEY) and ten years (TENY) – is used. The reason for taking G-Sec data is that this segment of money market is fairly developed in India (Bhattacharyya & Sensarma, 2016) and as we already discussed the success of monetary policy transmission depends on development of money market. In addition, as pointed by former RBI deputy governor, the G-Sec market serves as standard benchmark for pricing other market instruments; hence, it is pivotal in the transmission of monetary policy across the yield curve (Mohan, 2009). For lending rates, benchmark prime lending rate (BPLR) of the State Bank of India (SBI) is used as proxy. The reason for taking SBI BPLR as lending rate proxy is that SBI is the largest lender in India. The data for short and long-term interest rates is taken from Reserve Bank of India’s database on Indian economy. Data on SBI BPLR is taken from SBI. The descriptive statistics of variables used are reported in Table 1.
Table 1. Descriptive Statistics.
The empirical estimation is carried out by using nonlinear autoregressive distributed lag (NARDL) (Shin et al., 2014). The asymmetric ARDL (NARDL) model combines a nonlinear long-run relationship with nonlinear error correction by the use of carefully constructed partial sum decompositions. Consider the following asymmetric regression:
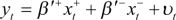 (1)
(1)
Where xt is a k ´ 1 vector of regressors decomposed as:
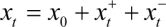
Where .png) and
and .png) are partial sum processes of positive and negative changes in xt defined by
are partial sum processes of positive and negative changes in xt defined by
 (2)
(2)
Where b+ and b– are the associated asymmetric long-run parameters. The asymmetric error correction model is:
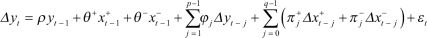 (3)
(3)
Where .png) and
and .png) .
.
In this framework, the procedure of testing follows as suggested by Shin et al. (2014), according to which ‘the non-standard bounds-based F-test of the null hypothesis t = i+ = i– = 0 can be applied to test for the existence of an asymmetric long-run levels relationship (Pesaran et al., 2001). Both long-run and short-run restrictions can be easily tested using standard Wald tests. This approach is valid irrespective of whether the regressors are I(0), I(1) or fractionally integrated.
The error-correction mechanism described by Equation 3 can have the following three special cases:
(i) Long-run symmetry where i = i+ = i–
(ii) Short-run symmetry in which .png) ; and
; and
(iii) The combination of long- and short-run symmetry in which case the model collapses to the standard symmetric ARDL model advanced by Pesaran and Shin (1999)’.
Additionally, the adjustment from a shock (short-run disequilibrium) to a new steady state long-run equilibrium is explained by dynamic multipliers whose cumulative asymmetric nature is expressed as:
 (4)
(4)
Where .png) and
and .png) tends toward the respective asymmetric long-run coefficients
tends toward the respective asymmetric long-run coefficients .png) and
and .png) , respectively, as h ® ¥. Here, xt is decomposed into
, respectively, as h ® ¥. Here, xt is decomposed into .png) and
and .png) about a zero-threshold value delineating the positive and negative changes in the growth rate of xt. This simple approach has an intuitive appeal and provides estimation results that may be easily interpreted.
about a zero-threshold value delineating the positive and negative changes in the growth rate of xt. This simple approach has an intuitive appeal and provides estimation results that may be easily interpreted.
The cointegration test applied to Equation 5, is an F-test on the joint hypothesis that the coefficients of the lagged level variables are jointly equal to zero. The general-to-specific approach is followed for the final NARDL specification. The preferred specification is chosen as suggested by various lag selection criteria’s and dropping all insignificant lags. The inclusion of insignificant lags may lead to imprecision in the estimation, which may introduce noise into the dynamic multipliers.
The following nonlinear error correction model is used for estimation:
 (5)
(5)
Where MPI is monetary policy index and Z is the vector of various interest rates used in the study which enters the estimation procedure alternatively.
Order of integration is less relevant for NARDL, albeit the variables should not be I(2) in which case the computed test statistics are not valid. Therefore, to ensure that none of the variables is integrated of order two, that is, I(2), it is important to check for unit root. We have used Ng and Perron (2001) unit root test, which is considered more robust compared to other unit root tests. The results reveal none of the variables is I(2) and the results are reported in Table 2. We also used Augmented Dickey–Fuller (ADF) and Dickey–Fuller Generalized Least Squares (DF-GLS) unit root tests.4 The results of these tests also corroborate the results of Ng and Perron (2001). Therefore, we may conclude that none of the variables used in the study is I(2).
Table 2. Ng-Perron Unit Root Tests.

The estimation procedure followed in this article differs from what has been widely followed in studying pass-through from policy rates to market interest rates. In this article, we will estimate the first stage of pass-through from policy rates (using MPI) to short-term rates where WACMR rate is the immediate target of monetary policy in India. In the second stage, instead of estimating pass-through from money market interest rates to lending rates as is standard practice in literature, we will estimate the pass-through directly from policy rates to long-term interest rates and lending rates. The reason is that due to presence of large state-owned banks and their role in the financial system, the standard two-stage pass-through framework does not work in India (Rajan & Yanamandra, 2015). Since we are using data for lending rates from the largest state-owned bank in India, it is appropriate that we follow the monetary policy approach of pass-through.
Monetary Policy Index
The RBI uses multiple instruments for the conduction of the monetary policy. These instruments can be broadly classified as price-based and quantity-based instruments. The price-based instruments are mainly directed to influence the cost-of-funds for financial institutions, e.g. repo rate and reverse repo rate. The quantity-based instruments like CRR and statutory liquidity ratio (SLR) are directed to affect the volume of funds available to financial institutions. Change in one of them or a simultaneous change in more than one instrument can lead to misinterpretation of the overall policy stance. For example, if repo rate is decreased with an increase in CRR, one wonders what the overall stance of monetary policy is. The overall impact of this kind of policy move depends on the cost adjustment capacity and liquidity availability position of financial institutions. In such a situation, it is difficult to identify a single instrument to be the main policy instrument. So, in order to overcome this problem, it becomes imperative to consider all these instruments to get a better picture of the overall policy stance. Hence, we developed a comprehensive index using PCA which includes these instruments for our analysis.
The monetary policy index (hereafter MPI) which we developed includes the data on repo rate, reverse repo rate, and CRR. The reason for exclusion of SLR is that from 1997 to 2008 SLR stayed constant at 25% and even after that it declined by less than 5%. In contrast other instruments show frequent changes. As pointed out by Mishra et al. (2016), lending response to SLR changes is very small as compared to CRR, and since there are fewer changes in SLR during our sample period, we dropped it from our analysis.
Empirical Results
We start our discussion with MPI. The results from PCA are reported in Table 3 and Table 4. From Table 3, it can be seen that component 1 explains about 68% of variation in the data, component 2 explains 29% and component 3 about 2%. The eigenvectors from Table 4 suggest that for only component 1 all the instrument weights are positive. Hence, we take component 1 as our index (MPI) for further analysis. In component 1, repo rate emerges to be the most important relative to reverse repo and CRR. Hence, we can conclude that during our analysis period, repo rate is the most important policy tool used by RBI to conduct the monetary policy operations.
Table 3. Principal Component Analysis.

Table 4. Principal Components (Eigenvectors).

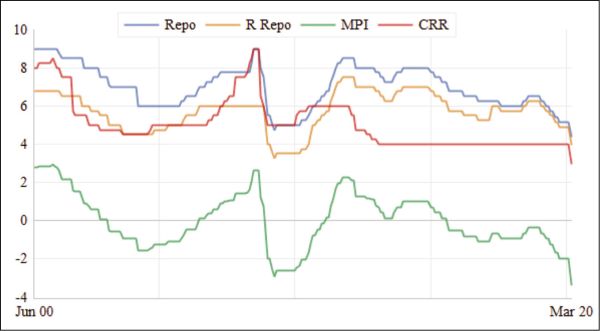
For a composite index to be representative of vector of variables, it is important that the index behaves the same way as individual components. In order to check this property, we plotted MPI with its individual components, that is, repo rate, reverse repo and CRR. Figure 1 shows the plot of MPI, repo, reverse repo and CRR. From Figure 1, it can be seen that MPI captures the policy stance as depicted by movements in other policy instruments. All the contractionary and expansionary phases are well captured. It can be seen that individual policy instruments also co-move in the same direction; thus, we may conclude that despite multiple objectives, no systematic policy decision bias is found in monetary policy of RBI.
Figure 1. Plot of MPI and Other Monetary Policy Instruments.
Now moving towards the results of interest rate pass-through. We start our analysis with the results of short-term interest rates – WACMR and TB. The results are reported in Table 5. The FPSS test confirms the existence of cointegration in both cases. The FPSS values in both cases exceed the upper critical value of 5.73 for k = 1, where k is number of independent or explanatory variables and does not take into account the decomposition of variables as positive and negative partial sums as required in NARDL.
The results of Wald test (Table 5) suggests rejection of long-run symmetry in both positive and negative cases. The Wald test statistics does not allow us to reject the null of short-run symmetry. The overall evidence, therefore, is absence of short-run asymmetry from MPI to short-term interest rates and presence of long-run asymmetry. The speed of adjustment is negative as expected. However, the adjustment speed for TB is less than WACMR. From the results in Table 5, it can be seen that MPI+ coefficient is unity in case of WACMR and close to unity in case of TB, which can be seen as complete pass-through from policy rate to short-term interest rates in case of a rate hike. In contrast the MPI- coefficients for WACMR (0.91) and TB (0.81) are below unity, which can be as incomplete pass-through from policy rates to short-term interest rates in case of a rate cut. Thus, the complete pass-through in case of rate hike and incomplete pass-through in case of rate cut is seen as asymmetric pass-through. The overall evidence suggests that RBI has been successful in achieving the primary goal. The weighted average of call rate is set on a daily basis by the interbank segment of call money market and this call rate is seen as operating target of RBI. As our results reveal RBI has been successful in aligning its operating tools with call rate thereby successfully regulating liquidity in the economy. Our results suggest that RBI has been successful in ensuring the efficacious transmission of policy changes to the first stage of interest rate term structures.
Table 5. NARDL Results for Short-term Interest Rates.
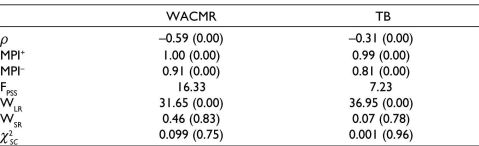
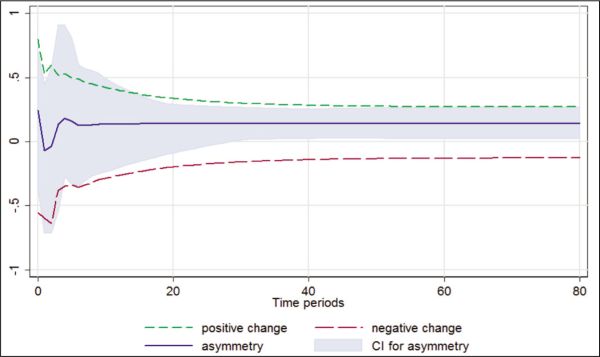
Figure 2 and Figure 3 show the dynamic effects of a unit negative/positive change in MPI on WACMR and TB. The blue line is the line of asymmetry. The value of this line at any given point indicates asymmetry at that point. From Figure 2 and Figure 3, it can be seen that there is only long-run asymmetry as the blue line shows that the response is asymmetric to both positive and negative changes. Over the long horizon, the response is asymmetric in both cases as WACMR as well as TB respond more to the positive changes as compared to negative changes thus confirming the presence of long-run asymmetry of positive nature. From the above figures, it can be seen that it takes nearly five to six months to reach new equilibrium from a shock.
Figure 2. Cumulative Effect of MPI on WACMR.

Note: 99% bootstrap CI is based on 100 replications.
Figure 3. Cumulative Effect of MPI on TB.

Note: 99% bootstrap CI is based on 100 replications.
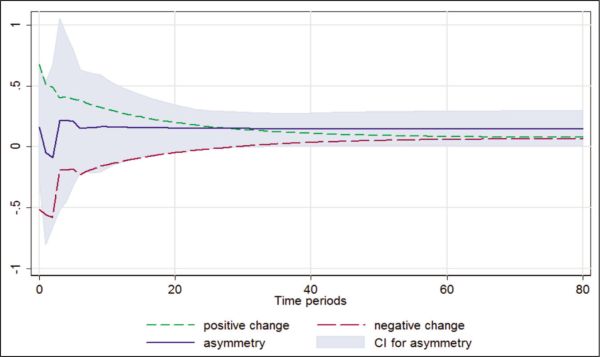
The results for long-term interest rates are presented in Table 6. The FPSS test confirms the existence of cointegration in both cases. The FPSS values in both cases exceed the upper critical value. The Wald test suggests rejection of long-run symmetry in all cases, hence the evidence of long-run asymmetry in all cases. The Wald test statistics does not allow us to reject the null of short-run symmetry. The overall evidence, therefore, is absence of short-run asymmetry and presence of long-run asymmetry. The results are similar to short-term interest rates as far as asymmetry is concerned. However, the remarked difference is that of pass-through coefficients. The pass-through coefficients decline with increasing maturity with the exception of MPI- for TENY. The coefficients of adjustment are negative and significant in all cases. However, the speed of adjustment declines with increasing maturity. From Table 6, it can be seen that the positive coefficients are larger than the negative ones with the same exception for TENY. These declining and different coefficients for MPI+ and MPI- are highly suggestive of incomplete and asymmetric pass-through from policy rates to long-term money market rates. The dynamic multipliers presented in Figures 4, 5, 6 and 7 show the presence of long-run positive asymmetry in all cases.
Table 6. NARDL Results for Long-term Interest Rates.

Figure 4. Cumulative Effect of MPI on ONEY.
Note: 99% bootstrap CI is based on 100 replications.
Figure 5. Cumulative Effect of MPI on THREEY.

Note: 99% bootstrap CI is based on 100 replications.
Figure 6. Cumulative Effect of MPI on FIVEY.
Note: 99% bootstrap CI is based on 100 replications.
Figure 7. Cumulative Effect of MPI on TENY.

Note: 99% bootstrap CI is based on 100 replications.
The overall picture of our results shows that between the short-end and the long-end of yield curve, the pass-through from policy rates varies significantly. As is clear from our results influence of monetary policy on short-term interest rates is significant, while in case of long-duration maturity interest rate-bearing securities the pass-through from policy rates declines as maturity increases. Thus, we can say monetary policy has a significant influence on short end of yield curve as compared to the long end. These results are in line with other notable studies in the area. Our results also show that there is noticeable asymmetry which shows substantial similarity across the vector of interest rates under study. We find the long-run response to monetary tightening is greater in absolute value than the response to monetary expansion of the same value. This kind of differential response to a rate hike and rate cut is dubbed as long-run positive asymmetry.
Our results have profound policy implications. The positive long-run asymmetry can be seen as limitation of monetary policy in lowering long-term inflationary expectations. It can also be seen as ability of monetary policy to slow down an overheated economy but inability to stimulate a slowing economy. Thus, the elucidation of a bygone epigram that one can pull a string but cannot push the same can be viewed as true for monetary policy as suggested by our results. The absolute larger response to rate hikes is an indication that monetary authorities have an advantage in preventing bubbles. This larger response to rate hikes prevents monetary authorities from weighty rate cuts necessary for preventing bubbles. However, the smaller response to rate cuts is of great contemplation from demand management perspective. When response of long-term interest rates to a rate cut is small, authorities need to make repeated cuts in order to have a substantial impact in order to stimulate the economy. As our results show that response to rate cuts is smaller than rate hike, under such conditions policymakers either have to make repeated cuts or have to make substantial cuts which may disturb the foreign exchange and financial markets by creating substantial volatility. Moreover, the condition of zero lower bound prohibits central banks from cutting rates beyond it, if the central bank has not resorted to unconventional measures of monetary policy.
The results for lending rates are presented in Table 7. The FPSS test confirms the existence of cointegrating relationship. As the estimated test statics value exceeds the upper critical value of 5.73 (for k = 1). The Wald test suggests rejection of null of long-run as well as short-run symmetry, hence the evidence of both long-run as well as short-run asymmetry. The results are different from those obtained for short-term and long-term interest rates as reported above. The pass-through coefficients for rate hike (0.77) are larger in absolute value than that of rate cut (0.40). This can be dubbed as positive long-run asymmetry. The coefficient of adjustment is negative and statistically significant. However, the small value (–0.15) of coefficient of adjustment suggests sluggish pass-through from policy rates to lending rates.
Table 7. NARDL Results for Lending Rates.

The dynamic multipliers presented in Figure 8 show the presence of both long-run and short-run positive asymmetry. As can be seen from Figure 8, lending rates respond more to positive changes in both short-run and in long-run. From the above figures, it can be seen that it takes nearly 15–18 months to reach new equilibrium from a shock.
Figure 8. Cumulative Effect of MPI on Lending Rates.

Note: 95% bootstrap CI is based on 100 replications.
The possible explanations for this slow, asymmetric and incomplete pass-through depend on many factors associated with the costs-of-funds of banks which may or may not be directly related to the policy decisions of central bank. One such explanation for positive short-run asymmetry is the gradual abrasion of the operating margin. Consider when central banks raise policy rates, if banks have sufficient margin, they will absorb this hike and will not pass the hike. On the other hand, if banks do not have enough margins to absorb the hike, they will have to adjust their cost-of-funds, so they will respond to these hikes by passing them on in order to be financially solvent in short-run. Over the long-time horizons if there is competition in the banking sector, banks will have to revive their rates and lower them. The absence of competition allows banks to maintain high rates and response to monetary loosening in such an environment is less effective. In other words, lending rates respond to rate cuts less as compared to rate hikes.
In the absence of banking regulations, commercial banks are free to determine the degree of pass-through from policy rates to their lending rates. These decisions on the extent of pass-through depend on an array of factors like costs-of-funds, liquidity management, market share of a particular bank and profit maximisation. Moreover, financial liberalisation has provided banks a safe haven in the form of access to foreign markets thereby allowing them to keep their margins intact without responding to changes in monetary policy which may alter their costs-of-funds or change their market share.
The greater availability of information by the advent of information technology boom has influenced the pricing strategy of banks dramatically. The borrowers have now greater information about financial market, so they have greater bargaining power in deciding among various borrowing arrangements. Additionally, borrowers face reduced or negligible switching and refinancing costs which make them more foot-loose.
Out of the probable explanations given above, we cannot identify the exact reason for our documented results as this is not the subject matter of this study. However, there are studies which have extensively worked on the impediments to pass-through in India. A closer examination of these studies may help us to corroborate our findings. One of these studies by RBI (2012) finds that increase in credit-deposit ratio5 and a decrease in cost-to-income6 ratio leads to an increase in the pass-through. The study finds that pass-through increases by 0.45 to 0.52 by a unit standard deviation increase in credit-deposit ratio and pass-through increases by 0.1 with a unit standard deviation decrease in cost-to-income ratio. In another study by RBI (2014), it was found that most of small savings in India are held in small saving schemes like post office savings, saving certificates etc. as compared to bank deposits. Since the rates on these small schemes are regulated, therefore, it weakens the bank lending channel of monetary policy. Rajan and Yanamandra (2015) in their study highlighted that fiscal dominance, bank concentration, inflation and pervasiveness of informal financial sector are major impediments to effective transmission.
Conclusion
In this article, we empirically studied the interest rate pass-through in India. We used data on short-term and long-term money market interest rates as well as lending rates data of SBI to study the pass-through in India. We used asymmetric ARDL model which has many advantages like examination of asymmetries of different nature.7 The findings of this study correspond to a certain period, the methodology used and the vector of interest rates studied. Therefore, the findings may change if any of these undergoes a change. Thus, the interpretation and generalising of these findings need to be done with certain caution. The main findings of this study can be summarised in three points.
First, our results suggest the rejection of decoupling hypothesis of interest rates, as we find evidence of cointegration between the policy rates and all other market interest rates. Second, we find evidence of near complete, relatively rapid and asymmetric pass-through from policy rates to the immediate monetary policy target in India, that is, call money rates. In addition, we find evidence of incomplete, sluggish and asymmetric pass-through from policy rates to long-term market interest rates. Third, we find evidence of incomplete, very sluggish and strong (short-run as well as long-run) asymmetric pass-through from policy rates to lending rates.
Given the evidence of incomplete, sluggish and asymmetric pass-through, it is implausible for a central bank to focus only on short-end of yield curve in anticipation that the long-end of the yield curve will follow suit.
In sum, given the complexities in the pass-through as evidenced, relying solely on a single channel or single tool for aggregate demand management by a central bank may not yield suitable results. This kind of policy environment warrants regulatory reform and/or developing more alternative and effective tools for monetary policy. These reforms can be regulation of financial institutions to strengthen them thereby strengthening the pass-through and developing new tools for aggregate demand management.
Declaration of Conflicting Interests
The author declared no potential conflicts of interest with respect to the research, authorship and/or publication of this article.
Funding
The author received no financial support for the research, authorship and/or publication of this article.
ORCID iD
Taufeeq Ajaz  https://orcid.org/0000-0001-5286-7755
https://orcid.org/0000-0001-5286-7755
Notes
1. Brazil, Russia, India and China.
2. India, Pakistan, Bangladesh and Sri Lanka.
3. Liquidity adjustment facility (LAF) was introduced in June 2000 for maintenance of liquidity in the economy on daily basis.
4. Results are not reported but are available on request.
5. Credit-deposit ratio is the ratio of the amount banks lend from the mobilised deposits. It is an important indicator of banking industry.
6. The cost-to-income ratio is an indicator of operating efficiency of banks. When operating costs are high, a rate cut from monetary authorities may not be passed to the lending rates as this extra earning can be used to manage the high operating costs or in other words to manage the costs of funds.
7. Here we are referring to asymmetries of short-run and long-run in nature.
Becker, R., Osborn, D. R., & Yildirim D. (2012). A threshold cointegration analysis of interest rate pass-through to UK mortgage rates. Economic Modelling, 29(6), 2504–2513. https://doi.org/10.1016/j.econmod.2012.08.004
Berger, A. N., & Gregory, F. U. (1992). Some evidence on the empirical significance of credit rationing. Journal of Political Economy, 100(5), 291–299. https://doi.org/10.1086/261851
Bernanke, B., Mark, G., & Simon G. (1996). The financial accelerator and the flight to quality. Review of Economics and Statistics, 78(1), 1–15. https://doi.org/10.2307/2109844
Bhattacharyya I., & Sensarma, R. (2008). How effective are monetary policy signals in India: Evidence from a SVAR model. Journal of Policy Modelling, 30(1), 169–183. https://doi.org/10.1016/j.jpolmod.2007.07.003
Borio, C. E. V., & Fritz, W. (1995). The response of short-term bank lending rates to policy rates: A cross-country perspective. In BIS (Eds.), Financial structure and the monetary transmission policy transmission mechanism (pp. 106–153). Basle. https://www.bis.org/publ/bppdf/bispap00c.pdf
Das, S. (2015). Monetary policy in India: Transmission to bank interest rates [IMF Working Paper, No. 15/129].
De Bondt, G. J. (2002). Retail bank interest rate pass-through: New evidence at the euro area level [Working Paper Series, European Central Bank, Frankfurt, Germany, No. 136].
De Bondt, G. J. (2005). Interest rate pass-through: Empirical results for the euro area. Germany Economic Review, 6(1), 37–78. https://doi.org/10.1111/j.1465-6485.2005.00121.x
Dueker, M. J. (2000). Are prime rate changes asymmetric? Federal Reserve Bank of St. Louis Review, 82(5), 33–40. https://doi.org/10.20955/r.82.33-40
Égert, B., Crespo-Cuaresma, J., & Thomas R. (2007). Interest rate pass-through in central and Eastern Europe: Reborn from ashes merely to pass-away. Journal of Policy Modelling, 29(2), 209–225. https://doi.org/10.1016/j.jpolmod.2007.01.005
Égert B., & Ronald, M. (2009). Monetary transmission mechanism in central and eastern Europe: Surveying the surveyable. Journal of Economic Survey, 23(2), 277–327. https://doi.org/10.1111/j.1467-6419.2008.00563.x
Francesco G., & José, M. M. (2015). Interest rate pass-through in the Dominican Republic [IMF Working Paper, No. 15/260].
Fried J., & Peter H. (1980). Credit rationing and implicit contract theory. Journal of Money, Credit, and Banking, 12(3), 471–487. https://doi.org/10.2307/1991722
Greenwood-Nimmo, M., Shin, Y., Treeck, T. V., & Yu, B. (2013). The decoupling of monetary policy from long-term rates in the U.S. during the Great Moderation, SSRN. https://doi.org/10.2139/ssrn.1894621
Gual, J. (1999). Deregulation, integration and market structure in European banking. Journal of the Japanese and International Economies, 13(4), 372–396. https://doi.org/10.1006/jjie.1999.0428
Guimaraes, R., & Ruiz-Arranz, M. (2009). Monetary transmission in Asia: Is it working? In Asia and Pacific. Regional Economic Outlook, IMF.
Hattari, R., Islam, M. S., & Rajan R. S. (2011). South Asia and the global financial crisis: Impact and monetary policy responses. In J. Raghbendra (Ed.), Handbook of South Asian Economies, Routledge.
Karagiannis, S., Panagopoulos Y., & Vlamis P. (2009). The emerging BRIC economies: Evidence from the interest rate transmission mechanism. Oxford Business and Economics Conference Program, St. Hugh’s College, Oxford University, United Kingdom.
Kwapil C., & Scharler J. (2006). Limited pass-through from policy to retail interest rates: Empirical evidence and macroeconomic implications (Oesterreichische Nationalbank, Monetary Policy and the Economy, No. Q4/06).
Lowe P., & Thomas R. (1992). Loan rate riskiness: Theory and evidence [Research Discussion Paper 9206]. Reserve Bank of Australia.
Mishra, P., Montiel, P., & Sengupta, R. (2016). Monetary transmission in developing countries: Evidence from India [IMF Working Paper, No. 16/167].
Mohan, R. (2009). Financial sector reforms and monetary policy: The Indian Experience. Revised version of paper presented at the Conference on Economic Policy in Asia at Stanford, organised by Stanford Center for International Development and Stanford Institute for Economic Policy Research, on 2 June 2006. https://www.bis.org/review/r060612d.pdf
Perron, P., & Ng, S. (2001). LAG length selection and the construction of unit root tests with good size and power. Econometrica, 69(06), 1519–1554. https://doi.org/10.1111/1468-0262.00256
Pesaran M. H., & Shin, Y. (1999). An autoregressive distributed lag modelling approach to cointegration analysis. In: S. Strom (Ed.), Econometrics and economic theory in the 20th century, The Ragnar Frisch Centennial Symposium. Cambridge University Press. https://doi.org/10.1017/CCOL521633230.011
Pesaran, M. H., Shin, Y., & Smith, R. J. (2001). Bounds testing approaches to the analysis of level relationships. Journal of Applied Econometrics, 16(3), 289–326. https://doi.org/10.1002/jae.616
Rajan R. S., & Yanamandra V. (2015). Effectiveness of monetary policy in India: The interest rate pass-through channel. In R. S. Rajan & V. Yanamandra (Eds.), Managing the macroeconomy: Monetary and exchange rate issues in India. Palgrave Macmillan. https://doi.org/10.1057/9781137534149
RBI. (2009). The Evolution of Monetary Policy-2003-04. Special edition of the Report on Currency and Finance, Vol. I.
RBI. (2012). Macroeconomic and monetary developments – price situation. https://rbidocs.rbi.org.in/rdocs/
RBI. (2014). Addressing Impediments to Transmission of Monetary Policy. In Report of the Expert Committee to Revise and Strengthen the Monetary Policy Framework. 41–54.
Rotemberg J. J., & Garth S. (1987). The relative rigidity of monopoly pricing. American Economic Review, 77(5), 917–926. http://www.jstor.org/stable/1810217
Sander, H., & Kleimeier, S. (2004). Convergence in Euro-zone retail banking? What interest rate pass-through tells us about monetary policy transmission, competition and integration? Journal of International Money and Finance, 23(3), 461–492. https://doi.org/10.1016/j.jimonfin.2004.02.001
Sellon, G. H. (2002). The changing U.S. financial system: Some implications for the monetary transmission mechanism. Economic Review Quarter 1, Federal Reserve Bank of Kansas City, 5–35.
Shin, Y., Yu, B. C., & Greenwood-Nimmo, M. (2014). Modelling asymmetric cointegration and dynamic multipliers in a nonlinear ARDL framework. In R. Sickels & W. Horrace (Eds), Festschrift in honor of Peter Schmidt: Econometric methods and applications (pp. 281–314). Springer. https://doi.org/10.1007/978-1-4899-8008-3_9
Singh, B. (2011). How asymmetric is the monetary policy transmission to financial markets in India? RBI Occasional Papers, 32/2.
Stiglitz, J. E., & Andrew, W. (1981). Credit rationing in markets with imperfect market information. American Economic Review, 71(3), 393–410. http://www.jstor.org/stable/1802787